Bitcoin Outperforming Most Long-term Models

“It was always my sitting” - Edwin Lefèvre

Bitcoin has been on a tear in the past year, rising about a factor of 10. Much of this rise has been fueled by institutional money entering into multibillion dollar Bitcoin positions, such as the repeated investments from Michael Saylor’s MicroStrategy treasury and from Elon Musk’s companies (Tesla, and possibly SpaceX). As a result the price action is substantially outperforming most models except for the very optimistic Stock-to-Flow model.

Future Supply and Lindy models

I have created the Future Supply Model, which is an integral version of the differential stock-to-flow supply driven model. I also gave the moniker Lindy model to a power law model vs. block time. These two models are described in Substack articles here: https://stephenperrenod.substack.com/p/bitcoins-future-supply-model and here: https://stephenperrenod.substack.com/p/bitcoins-lindy-model .

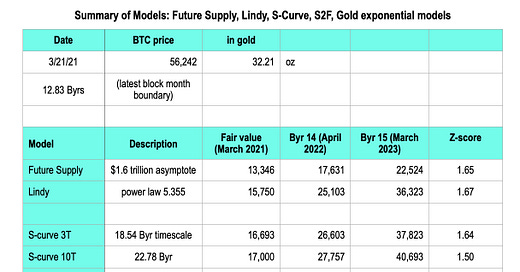
The models’ present day fair values and one and two year forecasts are summarized in the table below. All use 11 Block years’ worth of monthly data. This is the natural calendar system for Bitcoin given the Halvings and difficulty adjustment that are important price drivers. One Block year is 52,500 blocks, and typically runs about two weeks shorter than a calendar year. Currently just over 12.8 Block years have elapsed since Bitcoin was first created.

The Future Supply Model fair value is currently much lower, at $13,346 than the Bitcoin price of $56,242 today, March 21st, 2021. The Lindy model is also much lower at $15,750. However it must be understood that the long-term volatility of Bitcoin is large, with single standard deviations amounting to over factors of two up or down from trend.

This is captured in the Z-score, which measures the number of standard deviations of the current price above the model fair value at present. Each model indicates that price is above fair value by about one and two-thirds standard deviations, not yet stretched by two standard deviations.

I also show the model projections one and two block years into the future, when 14 block years have elapsed (April 2022) or 15 block years (March or April 2023). Even two years out the model projections are low compared to the current price.

S-curve models

Following the Future Supply model and Lindy model in the table, I show a family of S-curve models based on Weibull cumulative distribution functions. These are described in a Medium article here: https://medium.com/the-capital/bitcoins-long-term-value-e077e212264d. These models are three parameter models characterized by shape, timescale (shown in the Table above) and ultimate final value. I ran models for final values ranging from 1 to 100 trillion dollars (no future inflation assumptions included). In the table above the $3 trillion model is designated S-curve 3T, etc. One cannot statistically discriminate between the models at this point, although the higher ultimate market caps are very slightly favored.

It is still early days, as the time scale parameters of these models suggest.

One sees that these S-curve models have fair values at present around $17,000. Interestingly, for shorter times (shorter than the listed timescales) the first order approximation of the Weibull distribution looks like a power law in time, e.g. just like the Lindy model (but in market cap terms; the Lindy model in the table is a regression in terms of price). These models are less stretched, about 1.5 standard deviations.

A Stock-to-Flow model

Next I show fair value price for a stock-to-flow model based on market cap. PlanB uses both market cap and price in his models, I choose market cap for a better comparison to the Future Supply and S-curve models. If we calculate in Block years it is straightforward to analytically determine the instantaneous stock-to-flow per Block year, which was 56 at the last halving in May 2020 and is now about 56.83.

This regression of market cap vs. stock-to-flow is done on the same block monthly data (131 data points), it indicates a fair value of about $41,800, a power law on S2F of 3.28, and has a Z-score of one-third of a standard deviation. This is less optimistic than the “S2FX” model which uses clusters and also anchors explicitly to gold and silver. The precious metals represent 1/3 of just six data points in that model, thus effectively pulling that model toward a higher value than other stock-to-flow models.

Digital gold better

The last entry in the table is an exponential model of Bitcoin in gold ounces as a function of calendar year since the beginning of 2009. Bitcoin is currently at 32 ounces, and the model suggests a fair value of 14 ounces, so Bitcoin has been rising even faster than an exponential model. And the model is very steep, calling for a tripling of fair value within less than two years. Bitcoin has already exceeded the January 2022 projection, but of course things could change significantly for both gold and Bitcoin by then.

Kelly capital growth criterion

Also, I have updated the optimal Kelly fractional allocation calculation with latest data. Using a five year look back window of block monthly returns, a full Kelly allocation in a two asset USD and Bitcoin portfolio is 36%, as shown in the table. A half Kelly allocation is 18%. During the 5-year period 57% of the months were winning months for Bitcoin and the winning months outperformed the losing months by a large factor of 2.76.

Whether you look back five years or ten years makes little difference; a ten year look back window results in a full Kelly allocation of 35%. A large Kelly fraction occurs due to Bitcoin’s strong outperformance, but is tempered by the high volatility of Bitcoin, and the requirement of avoiding capital ruin.

Curb your enthusiasm?

Models are useful until they break. None of these models can be falsified at present. The S2F model is the most accurate of the set currently.  However the estimates of fair value from the other models suggests some curbing of enthusiasm is warranted.

We all root for the S2F model to continue to hold up for several more years and it appears to be doing very well in this Halving cycle, either in fiat terms or in gold terms. But eventually, perhaps by the end of this decade, it will break, since it is a power law of an exponential (S2F is exponential growing in time). It is highly divergent mathematically. Bitcoin might reach $1 million fairly easily (roughly corresponding to the USD money supply), but $1 billion will be beyond reach short of serious hyperinflation.

All wealth on the planet is “only” 400 trillion dollars, corresponding to some $20 million or so per Bitcoin if it consumed everything. Currently 0.25% of all wealth is in Bitcoin. A base monetary asset does not need to consume all wealth, it just has to provide a superior foundation for wealth to be priced in and transacted in through to final settlement. That would still require tens of trillions of dollars to compete with gold ($12 T) and US Treasury debt ($28 T), and for Bitcoin to be a reserve asset backing central bank digital currencies, as may develop in time.

This is not a sell recommendation. In this Substack article I showed that it is very difficult to outperform buy and hold with dollar cost averaging: https://stephenperrenod.substack.com/p/outperforming-buy-and-hold . Unless valuations get stretched to around two standard deviations above your favorite model, one should probably exercise restraint. 

Most readers are likely under allocated to Bitcoin based on the Kelly criterion or even half Kelly, so can consider adding on dips and regular dollar cost averaging. Of course a two asset Kelly calculation is not a substitute for a complete portfolio analysis when one may hold bonds, stocks, real estate, and other assets and income sources.

This is not investment advice. Bitcoin is highly volatile. Past performance of back-tested models is no assurance of future performance. Only invest what you can afford to lose. You must decide how much of your investment capital you are willing to risk with Bitcoin. No warranties are expressed or implied.