Grand Unified Theoretical Framework for Bitcoin #2

Testing against bubbles and waves

Review of the GUT framework

In my previous article I introduced a “GUT” framework for Bitcoin to address the shift toward institutional domination of net purchasing in the last several years. I built a Lagrangian of the form:

L = K + F - V

with a kinetic term K, a forcing function F, and a potential term V. The kinetic term is proportional to the square of the velocity, where the velocity is the temporal change in the log residuals. The potential term is a restoring spring-like term that pulls the behavior back toward the observed long term power law behavior. And the forcing function F reflects increases in capital inflows, less their offset by liquidity absorption within the Bitcoin marketplace.

https://stephenperrenod.substack.com/p/a-proposed-grand-unified-theoretical

In addition I imposed a constraint of the form

\( k = u \gamma + (c - \ell) = 5.83\)

in which u is the power law of the growth of addresses, γ is the Metcalfe’s network index, c is the flow rate for institutional capital, and ℓ is the liquidity absorption index. The first three u, γ, c are observed and ℓ is derived via the constraint toward long term price power law behavior with the observed index k.

We composed a dam analogy with Metcalfe’s network potential energy sitting behind the dam, and the idea that a self-organized critical state emerges as:

• Adoption supplies potential energy,

• Rails open spillways for capital to enter,

• Liquidity absorption dampens surges.

In other words, the kinetic response of price residuals, the pumping and regulation from channels and liquidity absorption, and the restoring spring force that drives bubbles and crashes back toward the power law together form the essence of this grand unified framework.

Equation of Motion

From differentiating the Lagrangian, the equation of motion becomes:

\(\ddot{\delta} + \kappa u \gamma \, \delta \;=\; \alpha \, \frac{d}{dt}(c - \ell)\)

where

• δ is the price residual from the power-law baseline,

• δ** is its acceleration,

• the left-hand side combines inertia and a restoring spring force,

• the right-hand side is driven by the time derivative of the pump (c - ℓ).

The resulting equation of motion captures all three effects: inertia of deviations, restoring forces pulling back toward equilibrium, and external pumping from capital flows. The observed long-term power-law index k = 5.83 reflects the balance of these terms, linking network growth, institutional channels, and liquidity dynamics into a unified framework.

This can be fit against the actual history of price residuals and their first and second temporal derivatives. It is more useful as a model when fitting to bubbles or significant waves of price departure from the main trend. Since the growth of institutional capital flows has been most pronounced in recent years, we show fits to to the bubble of 2021 and to the rapid price increase waves of 2024-2025.

Bubble of 2021

The y-axis graphs the acceleration, the second time derivative, of the log price residual during the bubble of 2021, defined as log10 price residual above 0.2, it lasted for 70 weeks with two peaks. The orange line is the fit to the observed values given by the blue line. The red line is the forcing from the capital pump and the green line is the restoring spring term.

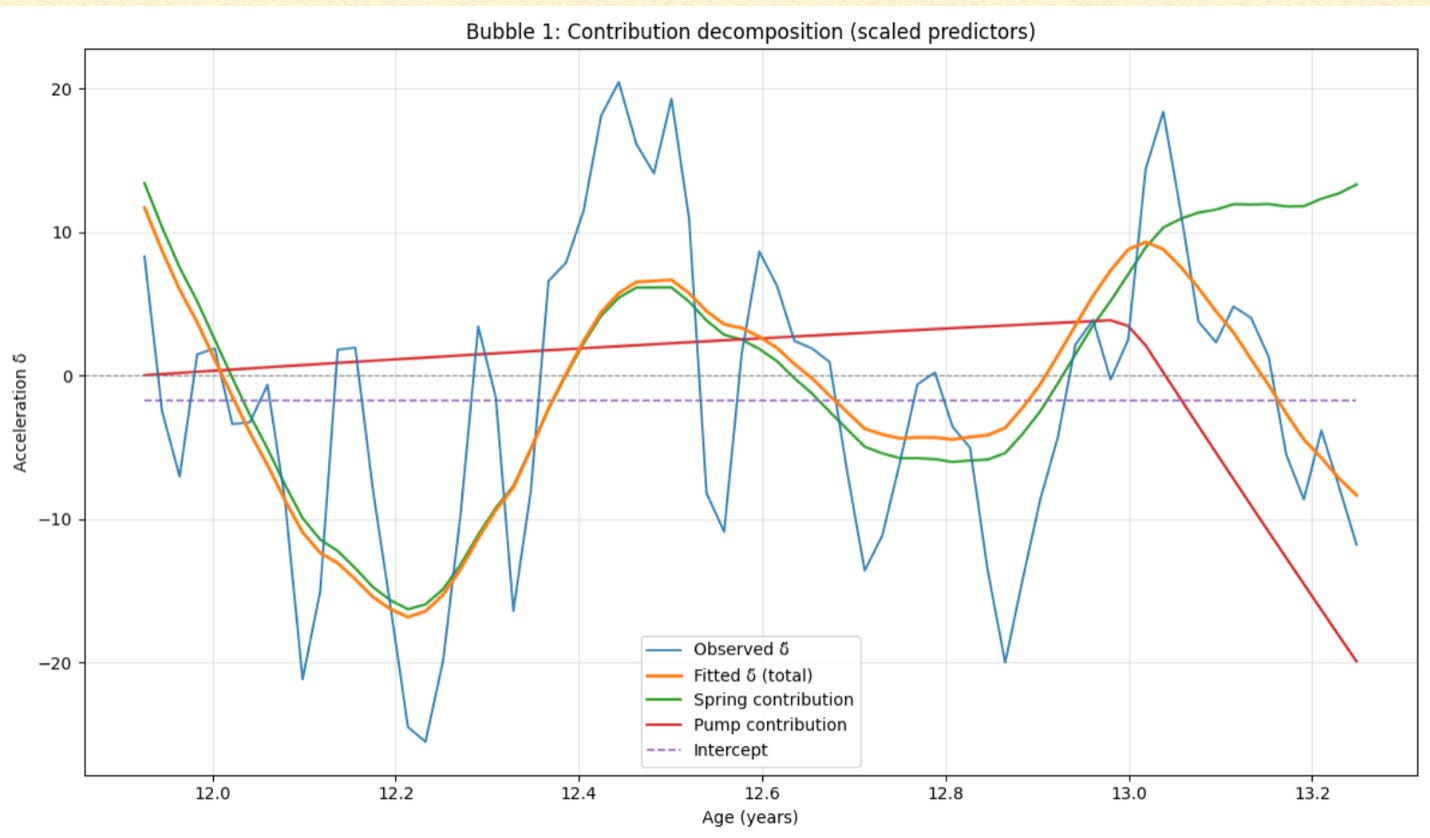
The fit is statistically significant, with both the spring and pump terms highly significant at 5 σ or better. The overall R² = 0.48 is quite acceptable.

• R² = 0.48 is quite decent, with residuals well behaved, probability random outcome very low at < 10^-7

• Spring κ’ = 8.55 (err 1.29, 6.6 σ)

• Pump α’ = -5.32 (err 1.09, 4.9 σ)

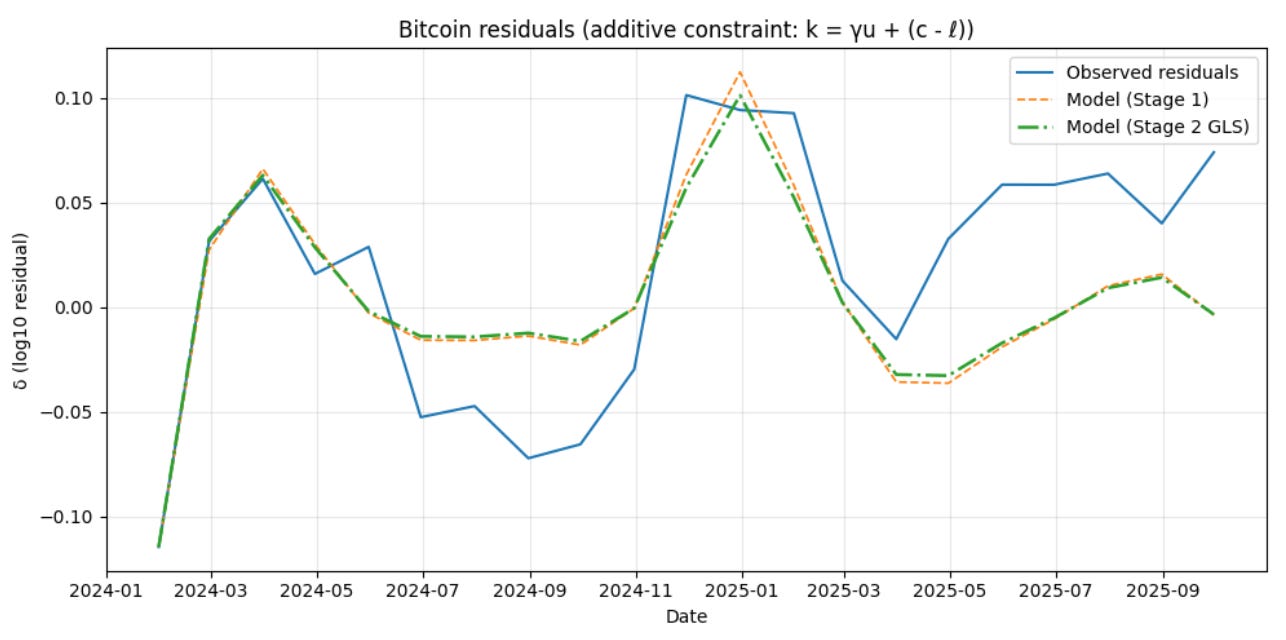
The Waves of 2024-2025

We have not had a major bubble since the 2021 bubble. But nevertheless we checked the model against the waves in the 2024-2025 interval. First we gathered the monthly values for the increase in total institutional holdings, and then differentiated that series to determine the c values, the local power law index for the flow, the additional holdings for the month in question. That series is noisy with a median value of 4.2, but a standard deviation near 7.1, and 10% of the values were less than zero. The u and γ values are the average measured for the interval in question.

The chart below shows the fit of the model to the observed log10 price residuals during 2024 and most of 2025. The fit is rather good with an R² of 0.53.

The modest wave action of 2024-2025 and a fit of the model to those, resulted in significant R² = 0.53. The yellow dashed line is the model, and the green dashed-dotted is a small tweak of generalized least squares, and only slightly different. The blue line traces the monthly observed residuals, all are in the range of -0.1 to 0.1 in log10 price, not large enough to count as a typical bubble historically. The first wave was the ETF wave of early 2024 and the second wave the post-2024 US election wave.

Swissblock’s Bitcoin liquidity index. There is a nice correlation between the Bitcoin residual plot and model fit and this BTC liquidity index. Theirs is a proprietary micro-liquidity index specific to Bitcoin, not a macroeconomic liquidity index.

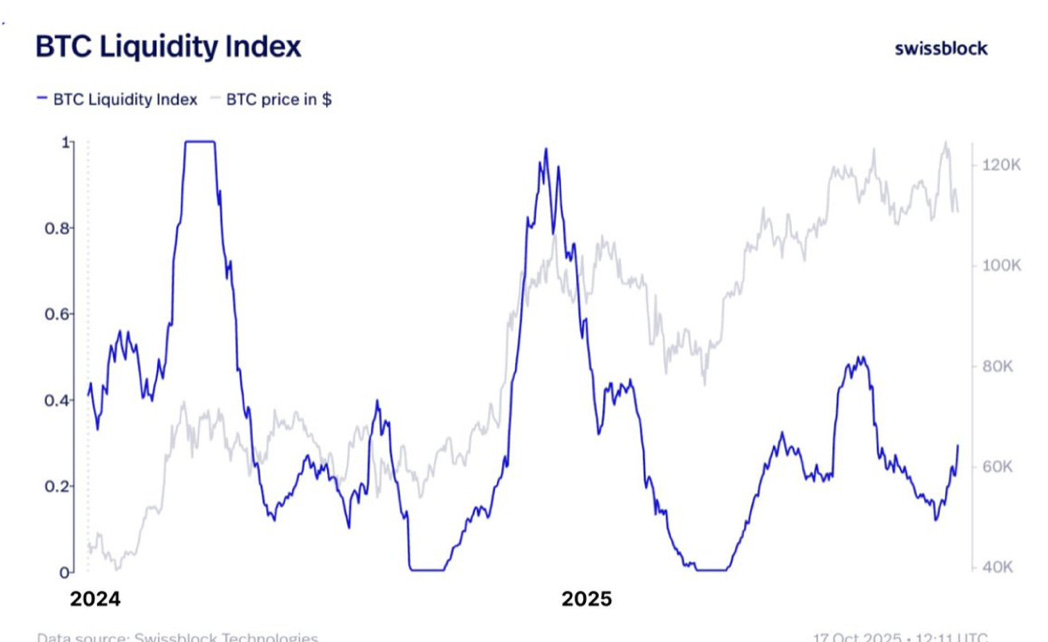
The final chart is Swissblock’s Bitcoin micro-liquidity index that correlates in general terms with the residuals and the model fit.

Summary

The physically motivated model for capital flows and liquidity absorption, modeled as a forced harmonic oscillator with spring restoration to the long term power law, provides a decent fit to both the 2021 bubble and the 2024-24 less volatile wave action.

The models explain about half of the variability, at least when using monthly interval data on the capital inflow. It is meant to be an overall theoretical framework, providing insight into Bitcoin dynamics as institutional flows have come to dominate, but not a model for precise prediction.