Bitcoin Long-term Update, July 2022

Six models agree fair value above $30,000

This is not investment advice. Bitcoin is highly volatile. Past performance of back-tested models is no assurance of future performance. Only invest what you can afford to lose. You must decide how much of your investment capital you are willing to risk with Bitcoin. No warranties are expressed or implied.

This article updates fair value prices and intermediate term projections for six long-term Bitcoin valuation models. All six models are good fits to the over 12 years of monthly data, but a Lindy power law model regression of market cap and a $100 trillion ultimate value S-curve model are the two best performing ones.

Models run over 12 Block years

For all models I perform regressions over a 12.17 Block year period running from 2 elapsed Block years until the present, and with 147 Block monthly observations. Bitcoin has its own natural calendar due to the halvings each four years and difficulty adjustments each fortnight, so it is natural to regress in such a calendar, especially for the supply-based models. Currently there is little difference with the Gregorian calendar year being only a few days longer than the Bitcoin Block year of 52,500 blocks.

Table 1. Six long-term models for bitcoin price and market cap. Market cap is currently about 19.09 million times the Bitcoin price, based on the already mined supply. All models are regressed in block calendar terms with Block years consisting of 52,500 blocks, using monthly data, and have 147 data points covering the interval from 2 to 14.17 elapsed Block years. We estimate fair value now and one year from now based on the regressions and calculate the expected one year growth in fair value. The Z-score is the number of standard deviations by which the current price is above or below the model price; standard deviations are calculated in log price or log market cap terms. The soft floor is the Z = -1 price, and represents possible downside support.

The methodology for the first four models in Table 1 is described in this article:

https://medium.com/the-capital/the-future-supply-model-era-4-ca3e9591d871 .

Lindy technology persistence (power law) models

The Lindy model is my name for a power law of block time model, and can be regressed in either price or market cap. Lindy refers to the technology persistence effect; the longer technology has been around, the longer its expected future lifetime and the more market share it grabs from the old technology. In the case of Bitcoin, the pre-existing technologies are gold and fiat currencies. 

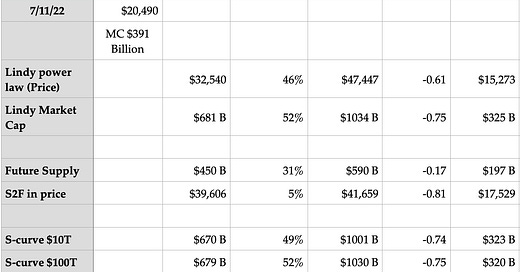
We find a current fair value price of $32,540 for the Lindy model and a one year growth rate of 46% leading to a one year projection of fair value around $47,450. The current Z-score is -0.61, and a short-term fall to Z = -1 would be to around the $15,270 price level. For the market cap version the growth rate of market cap fair value is 52% over the next year and the Z-score -0.75. Divide market cap by 19.09 million to convert to price.

Here is the Lindy model showing the log10 of market cap regressed against the log10 of block years elapsed. It has the best statistics of the six models covered in this article.

Figure 1. Regression of the market cap of Bitcoin (B$) since it was two years old, against age of the blockchain in block years. This is a log-log regression, or Lindy power law model, with power law index of 6.13. Market cap has risen faster than the 6th power of time. The green dashed lines are two standard deviations removed from the best fit; a standard deviation is a factor of 2.1 in linear terms (0.742 in the natural log). The positive skew is easily seen with the lower dashed line never pierced, but the upper dashed line pierced on three occasions. R-squared for this regression is 0.95. Regression performed in StatPlus.

Supply models

I introduced the Future Supply Model (FSM) as an alternative to the stock-to-flow model. The latter is a power law of a Stock-to-flow (S2F) that more than doubles at each halving, and is thus mathematically divergent, it heads toward infinity quite rapidly. Stock-to-flow is a differential formulation that has price (or market cap) dependent on the rate of change of supply. The FSM uses instead the integral formation, looking at the total of all future available supply of not-yet-mined Bitcoin. It converges to a finite ultimate market cap in the long term.

The FSM has a 31% growth outlook with a lower fair value market cap of $450 billion (corresponding to a fair value price level of $23,571), in comparison to S2F. It also has an ultimate market cap in the future of about $2.2 trillion (think of that as being in 2022 dollars, uncorrected for future inflation). It has a Z-score of -0.17 since its fair value is closer to the present day market cap of $391 billion.

For the Stock-to-flow model I also use Block monthly data. It is quite straightforward to directly calculate stock-to-flow for each block month, and thus is a more natural basis in which to perform such regressions; short-term variations in block times are smoothed out. The method is described in the article referenced above.

“As each new era begins, the forward-looking annual S2F = 2^(E+2)-8” where E is the era number, and currently E = 4.

Note that over the next year the fair value increase with the S2F model is a modest 5%. This is because all the action with S2F occurs at halvings, when S2F doubles (the inflation rate halves) and this drives a quantum shock to price. In between halvings, and we are currently just past the midpoint, S2F changes only slowly.

S-curve (Weibull) models

The S-curve models use a Weibull cumulative distribution function formulation. The methodology for that model is shown here in a Substack article. These are three parameter models that have a saturation time scale, a power law like scaling factor, and a terminal market cap value that must be assumed in order to determine the other two parameters through a double logarithmic transformation to a linear regression analysis. 

Here we show results for an ultimate market cap of $10 trillion (roughly equal to the value of all gold which is some $12 trillion) and for a $100 trillion market cap (roughly equal to the global M2 money supply).

The two S-curve models give similar results, which is another way of saying that the two different versions do not yet have predictive power around the ultimate market cap for Bitcoin. Will it challenge all gold? And will it go on to challenge all fiat currency? Nevertheless the higher ultimate value $100 trillion model has slightly better regression statistics than the $10 trillion one.

Table 2. Model statistics for the six models. All models give good fits to the data, but the best R^2 (correlation squared) and F-test scores are from the Lindy Market Cap model and the S-curve model with ultimate market cap $100 trillion.

Table 2 summarizes the statistics for the three models and we see the Lindy model and the $100 trillion S-curve have the highest R^2 correlation squared and F-test values. Since at early times the Weibull cumulative distribution function used in the S-curve model reduces to a power law in first order, it is not surprising that they have close agreement.

All models have very respectable R^2 and F-test values. Note also the standard deviations, which are in log (price or market cap) terms. They are log10 for the first four models and natural logarithm based for the S-curve models as the easiest way to formulate. In all cases the standard deviations are higher than a factor of 2.

Thus for example, for the first Lindy model, the standard deviation is 0.329 in log10, or a factor of 2.13. So if the fair value price is currently $32,540, the one sigma range is [$15277 , $69310]. From a long term statistical point of view there is nothing unusual about Bitcoin’s high in November 2021 around $69,000 nor if price were to drop to $15,000 in the current Crypto winter and technology stock recession. That is the volatility profile that one needs to prepare for, size for, and risk manage.

Geometric averages for each model category

Table 3. Geometric averages for fair value and one year projections for the two Lindy models, the two supply based models (Future Supply and Stock-to-Flow), and for the two S-curve models. The Lindy models and S-curve models are in approximate agreement with current fair value around $35,000 and one year projection in the low $50,000 area; both have 48% expected growth in fair value over the next Block year.

We can take geometric averages for each category of model: Lindy, Supply-based, and S-curve models. The conversion between market cap and price has been made with current supply and with the total Bitcoin supply one Block year from now, which is precisely known since it is 52,500 blocks of 6.25 Bitcoins in the future.

We find the Lindy and S-curve models are in good agreement; both have a current fair value in the mid $30,000s and with a one-year expected future fair value in the low $50,000s, and a growth rate of 48% in fair value.

The Supply average fair value is lower, since the Future Supply model is much more conservative. Also the S2F model will experience a big jump in May 2024 when the fourth halving arrives.

Summary

If the fair value is $35,000, buying $20,000 Bitcoin now and waiting a year until the fair value is around $50,000 seems like a pretty good deal. Bitcoin should begin to rise back toward fair value as we hit the bottom of this growth recession or actual recession, perhaps toward the end of this year. By May 2023 it will be just one year before the fourth halving and we will be entering a typically favorable part of the four-year cycle.

You could just keep dollar cost averaging, especially now, with substantially negative Z-scores indicative of low and favorable prices. Bitcoin is long-term savings technology.