Bitcoin's Long Term Value

Technology Adoption S-Curve model

This is not investment advice. Bitcoin is highly volatile. Past performance of back-tested models is no assurance of future performance. Only invest what you can afford to lose. You must decide how much of your investment capital you are willing to risk with Bitcoin. No warranties are expressed or implied. 

S-curve model for breakthrough Monetary technology

Bitcoin is a breakthrough monetary technology, and represents a pristine final settlement asset for cryptocurrencies in general. Like any major new technology it is expected to follow a technology adoption S-curve. Here we measure the adoption using market capitalization, this reflects both the number of users and the intensity of their allocation to Bitcoin, considering both individual investors and investment funds, as well as corporations such as MicroStrategy. Even nations are starting to invest in Bitcoin, El Salvador being the most notable example, but also sovereign wealth funds.

The most popular model for Bitcoin long-term valuation is the stock-to-flow model but it suffers from mathematical divergence and will almost surely break down this decade. It is a power law in stock-to-flow which itself is essentially an exponential function of time (two to a power).

What is more suitable is an S-curve style function that has rapid growth in the early stages (as Bitcoin has clearly shown), followed by slower growth, and then a flattening climb toward an ultimate value. That ultimate value should be thought of in real terms and might be equivalent to all gold ($12 trillion currently) or all M2 money supply or some lesser, intermediate, or larger value depending on how successful Bitcoin is as a monetary asset and substitution for gold, fiat currency, Treasury securities and other stores of value.

It turns out that a Weibull cumulative distribution function is very suitable for our purposes. It meets the above criteria and has been used in a wide range of engineering and even financial modeling instances, including the adoption rate of Internet banking technology as one example.

Block time

I measure time in Block years elapsed since Bitcoin began in 2009. Each block year is 52,500 ten-minute blocks in duration. Bitcoin has supply shocks or halvings each four years or 210,000 blocks, so modeling in Block years better reflects those key events.

Block years, by Satoshi’s design, are close to a regular calendar year, but run a little bit faster in practice. A Block month is 4375 blocks in length, 1/12 of a Block year. There are four such years between each Halving of the block reward subsidy that pushes up stock-to-flow and ensures a finite Bitcoin maximum supply of 21 million.

Weibull cumulative distribution function

The Weibull cumulative distribution function (CDF) can be written as:

f(t) = 1 - exp [ -(t/c)^k ]

where t is measured in Block years as described above. There are three parameters with the Weibull CFD. The first is a normalization parameter for the ultimate long-term market capitalization of Bitcoin from its continued price rise, and some incremental supply up to the 21 million maximum limit. This long-term capitalization, from a monetary technology standpoint, could ultimately be competitive with gold, Treasury bills, and global M2 fiat money. When the maximal market cap is reached, f = 1.

The second parameter, c, is the characteristic time scale. For any value of k, f(x) = 1 - 1/e = 0.632 at time t = c. This represents where the S-curve begins to flatten. The parameter k is the shape parameter, and for t « c serves as a power law index. At early times well shorter than the characteristic time, one approximates exp(-x) by 1-x and thus f(t) ~ (t/c)^k, a power law.

By applying a trick of taking the double log of f(t) one can linearize the equation and do a linear regression on the transformed version. After taking the natural log of both sides we have:

ln [1 - f(t)] = - (t/c)^k

and repeating,

ln (-ln [1-f(t)]) = k ln (t/c) = k * ln t - k * ln c .

If we identify the left hand side as y and set x = ln t, we have a linear regression of the form y = mx + b with m = k and b = -k* ln c. Performing a best-fit allows us to determine the parameters k and c.

Best fit for $30 Trillion case

Figure 1a. Regression of the double log of f, here denoted y, where the S-curve function f is the fraction of ultimate market cap reached by time t. We model with the Weibull cumulative distribution function which allows for this linearized regression “trick”. The function is such that when y =0 the curve is approaching saturation with f = 0.632, the market cap has reached 63.2% of its ultimate value. At early times the fraction f behaves like (t/c)^k, a power law with characteristic time c and power law index k. One sees that we are well below the saturation or flattening point at present (as f approaches one, y becomes positive and can be arbitrarily large).

The first figure reflects 139 Block monthly data points in a (natural log based) regression of y = ln (-ln (1-f)) against x = ln (Block years elapsed), where f is the fraction of ultimate market cap. The fit for this case is very good, with an r-squared value of 0.945, and an F-test value of 2352.

With this transformation we see a straight line fit in this double log (ordinate) vs. single log (abscissa) plot. Below, figure 1b, is what the best fit curve, and also a forecast, looks like in linear terms, using the optimal parameters k = 6.11 and c = 26.44 Block years. We have translated Block years into (estimated) calendar years for this graph. Obviously, if we are going to $30 trillion we are still very early, at around $1 trillion currently.

Figure 1b. S-curve forecast for $30 trillion best-fit case. We see a power law shape in the early years followed by a roughly linear portion from 2029 and then flattening starting around $19 or $20 trillion in 2034.

Four Market Cap choices: $3T, $10T, $30T, $100T

Since we are so early on the curve, in the power-law portion, we cannot distinguish between different assumptions around the ultimate market cap. So we look at four possibilities, separated by about a factor of 3 from one to the next: $3 trillion, $10 trillion, $30 trillion, and $100 trillion. The $3 trillion case exceeds gold held by all governments, and the $10 trillion choice is roughly comparable to all gold. The $30 trillion case exceeds the US M2 money supply (and cumulative budget deficit) and the $100 trillion case corresponds to global M2 money across the fiat universe.

In Table 1, I summarize the best fit parameters for the four cases and for a Lindy-style power law that is a good approximation at early times t << c (the time scale shown in the third column). The models are self-similar, in particular all reach 63.2% of ultimate value when the time elapsed equals the characteristic timescale c. Note all models have nearly the same shape parameter k, but longer time scales as the ultimate market cap increases.

Table 1: S-curve parameters for four values of ultimate market capitalization. We also include the Lindy power law which is a good approximation for times prior to the characteristic time scale shown in the third column. The shape parameter in the second column is identical to the power law index when the Lindy model applies at early times. All models have similar correlation coefficients and F-values, with a slight edge to the $100 trillion model. In the penultimate column we show the year at which the S-curve would flatten, as market cap reaches 63.2% of the ultimate value (= 1 - 1/e). The final column shows the approximate model price level corresponding to that market cap.

Thus the price level at flattening is 63.2% of the ultimate market cap divided by the projected supply of Bitcoin for the flattening year that is shown in the next to last column. We add the characteristic time scale in Block years to 2009 when Bitcoin’s first block was recorded, and correct for the average shorter length of Block years compared to calendar years of about two weeks.

Figure 2. This figure shows 5 years of market cap history and 14 years of future projection, at one year intervals, for each of four model regressions and actual market cap. The y-axis is logarithmic (marked in base 10). The actual market cap at the start of each year is shown with the blue curve, and the 2022 January 1 value is estimated with the present late November 2021 market cap. Note that the curves flatten earlier for lower market caps. In the case of the $100 trillion market cap, the 2035 value of around $30 trillion is only about a third of the ultimate value.

In Figure 2 we show the historical fit and forecast based on full data set (from 2 to 13.5 Block Years elapsed) since 2011 (not all of the low market cap history is shown here). The 2022 January 1st data point is estimated with the current $1.1 trillion market cap in late November. The current market cap is around factor of two above the best fit curves. But residuals are large, the corresponding Z-score (# of deviations above the prediction) is at present about 1.2 for any of the models, not especially on the high side since the maximum observed Z is 2.5.

For the first 15 or so Block Years (until 2024) all are well approximated by a Lindy power law model with power law index of 6.11. Flattening of the curves at 63.2% of peak occurs in 2026, 2030, 2034, and 2039 (not shown) for the $3T, $10T, $30T, and $100T models, respectively.

Latest 5 years of data

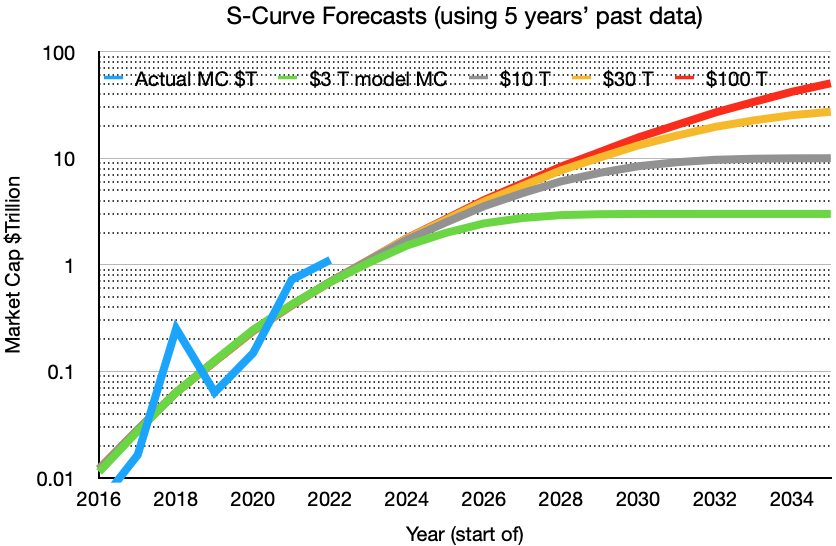
Now let’s look at just the past 5 years of history and see how this changes the regression results. We see an even stronger trend and a faster rise of the forecast curves. Figure 3 shows the historical fit and forecast based on just five Block years’ data since 2016, reflecting the stronger price performance of Bitcoin during this period. The power law portion has a steeper index of around 6.75, and the characteristic time scale is shortened by one and half ($3T) to three and half ($100T) years. This regression has lower statistical validity than the full data set, with F = 144, r-squared = 0.71. Still, it rejects the null hypothesis of no S-curve like trend easily.

Figure 3. S-curve forecast best recent history fit and projections with just the prior 5 years of data (on a Block monthly interval). These models have stronger performance with the $100 trillion case rising to $50 trillion by 2035 and the $30 trillion case saturating by 2035.

Summary of characteristic time scales

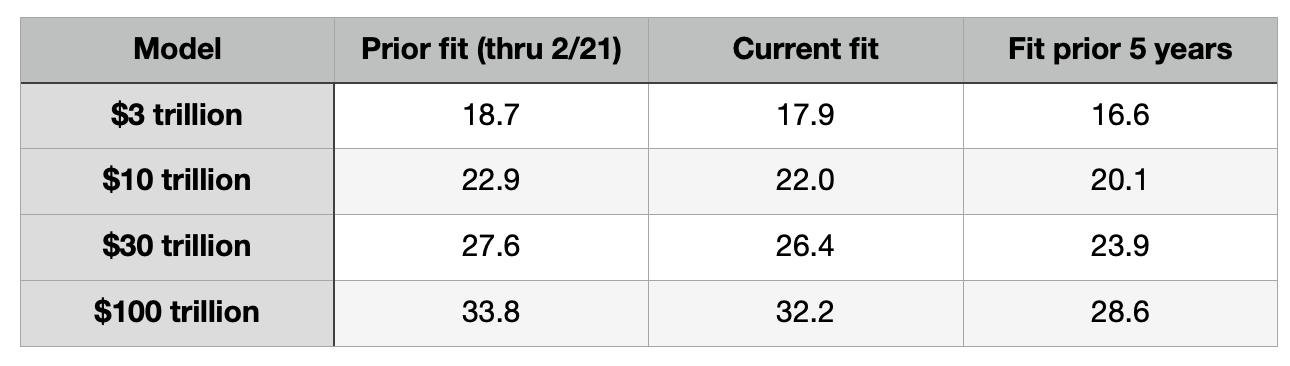
Table 2. Characteristic time scale in Block years for flattening of S-curve for different models. The second column has results from the March article, the third column the current best fit for time scale, and the last column the time scale estimate including only the prior 5 years worth of market cap behavior. The starting point is in January 2009, and we are now at 13.5 Block years elapsed. As an example, for the current fit to all data there are 22 - 13.5 = 8.5 Block years until the curve would flatten for the $10 trillion case, and 26.4 - 13.5 = 12.9 Block years remaining until flattening for the $30 trillion case.

In Table 2 we compare the characteristic time scale c for the model regressions. The second column has the fit parameters with available data through February 2021, as described in a previous article and analysis that appeared in Medium in early March. The third column has the current fit with data through early November 2021. And the final column only uses the last 5 years of data.

Conclusions

This analysis suggests we have 5 to 15 years or more of steep rise ahead of us in the market cap of Bitcoin. One subtracts 13.5, the current number of elapsed Block years, from the values in Table 2 to estimate when the knee (flattening) of the S-curve could be reached.

Since early in 2021, the characteristic time scale has shortened by 0.8 to 1.6 years depending on the ultimate market cap value, as a reflection of the strong performance of Bitcoin during most of this year. If you evaluate the prior five years only, there is an additional shortening of the time scale of 1.3 to 3.6 fewer years! If that effect persists (we could lose some ground if there is another “crypto winter”) we are talking about two to five years of speed up in the adoption and climb towards higher market cap.

Now one could argue that Bitcoin will never stop increasing in price measured against US dollars, since inflation of the Bitcoin supply is headed to zero and inflation of the US dollar supply is unending (and currently in the 6% range for CPI). Certainly continued USD inflation is likely, so one should interpret the models in terms of current 2021 dollars. Correcting for future US inflation is problematic, a fools errand, but until the characteristic time scale is reached, it is most likely a smaller effect than Bitcoin’s rapid climb in fair value which is currently projected to double each 1.6 years (55% per annum compounded).

While we cannot yet distinguish statistically between the four cases, it’s looking better than ever for the higher valuations above a $10 trillion long term market cap. The r-squared and F-test parameters have improved reflecting the strong recent performance and additional data points from the past nine months. And the model with the largest F value is the $100 trillion case. Bitcoin’s price behavior is outperforming all of these models for now; visual inspection of Figures 2 and 3 suggest it won’t be stopping at only a $3 trillion market cap.