Skew, kurtosis, and more
The moments of a price series are based on the means of simple power law functions rq, where r is the vector of daily (or some other chosen periodicity) returns for each time interval of the series and q, an integer, is the moment of interest. For q > 1, one is measuring the various degrees of how extreme price variations are, and which way they lean.
Moment q equation (normalized) S(q) = <rq> / σq
One generally takes r as the set of natural log returns for each time period, that is, ln (price today / price yesterday), for example. Then one determines the mean <rq> for the entire time series of interest.
For q = 2 we have the variance (whose square root is the standard deviation), and q =3 is the skew, positive if the right tail of the distribution is stronger, negative otherwise. The q = 4 moment, the kurtosis, measures whether the distribution is wider (if the normalized value > 3) or narrower (< 3) than a normal or Gaussian distribution. And the higher moments q =5 and q = 6 are known as the hyperskew (can be positive or negative) and hyperkurtosis (always positive).
Stock market returns generally have negative skew, that is enhanced downside (and crash) risk on top of their overall long-term exponential growth. Gold has positive skew, which is part of its appeal for diversification purposes. The paper linked earlier in this paragraph (‘negative skew’) found over a 53-year period, that skew for the S&P 500 was -0.62 and kurtosis 20.68. Another paper found for the 1982 - 2001 period, that skew was -2.39 and kurtosis 53.6 for the S&P 500. (But if the 1987 crash was excluded kurtosis dropped to just 6.8).
In both of these studies stock market skew was negative and the kurtosis was unfavorable, large relative to the expected value of 3 for a Gaussian distribution.
Bitcoin skew, kurtosis prior work
Two recent papers, both published earlier this year, one by Zhou of the University of Manchester, and another by Xu of Vanderbilt University, examined Bitcoin’s skew and kurtosis.
However, having done that, they each recommended low allocations to Bitcoin in comparison to ETF assets SPY, QQQ, GLD (gold), and DXY (dollar index). Xu concluded 5% or less and Zhou said less than 20% for a Bitcoin allocation within such a portfolio.
Interestingly, although both used daily data from October 2017 to January 2023, they found rather different results for skew and kurtosis. Zhou found 0.02 for the skew and 2.66 for the kurtosis of Bitcoin. Whereas Xu found 0.30 and 6.09, respectively. It seems both authors took the return as the delta price over price ratio, rather than the log of returns. They both normalized skew to the 3rd power and kurtosis to the 4th power of the standard deviation, as is frequent practice, and as shown in the equation below the title of this article.
The primary reason why their allocations are so low is they end up optimizing the Sharpe ratio of the four assets plus cash portfolios and they have no awareness of the power law nature of Bitcoin. As a result they end up with a noisier time series of residuals and also distort the skew and kurtosis, relative to the actual long term returns.
Bitcoin skew, kurtosis with log return residuals
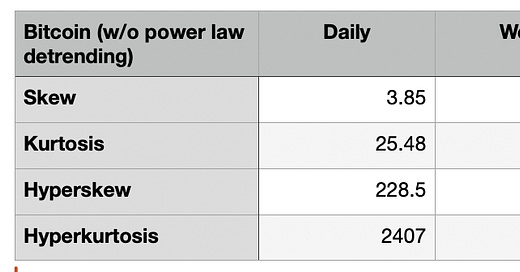
In Table 1, I show the normalized third through sixth moment values for Bitcoin using different time steps, either daily or weekly or monthly. These are results from the conventional method, using daily or other interval log returns. By definition the normalized variance takes the value 1.0. Notice there is significant variation in the values depending on the sampling rate, and that the signs can switch. The 4th through 6th moments are all rather high in each case, not surprisingly, for what we know to be a volatile asset

Bitcoin skew, kurtosis when Power law detrended
However, we know that Bitcoin adheres to a power law in the long term, and the technique of taking the series of fractional or log residuals does not account for that nature. So instead I looked at what happened if we use the log residuals relative to the expected value from the power law.
The best fit power law trend to the daily price series is
Log Price = -2.175 + 5.867 * Log (Age).
Here price is in USD, Age is the age of Bitcoin in years, the logs are log base 10, and the median value of a quantile regression method is used to determine the power law slope of 5.87, with pseudo R2 of 0.95.

Then I determine the normalized moments based on the full series of power law detrended residuals, by calculating log (price/trend expected price) at each point.
The moments calculated after power law detrending are drastically reduced, as shown in Figure 1. This plots the log of the moment value on the y-axis; one can see that the reductions are very significant, by up to a factor of 10 or more.
The new values for the 2nd, 3rd, 4th, 5th, and 6th moments are 1.94, 5.37, 14.9, 54.74 for the daily series, substantially lower than the daily column in Table 1, and more similar to the monthly values. This power law detrended dataset indicates a more stable investment environment than one would have otherwise concluded for Bitcoin.
Once you accept the reality of the very strong and persistent power law nature of Bitcoin, as has been demonstrated with its very high Hurst exponent of > 0.9 (https://stephenperrenod.substack.com/p/bitcoins-strong-persistence), the resulting higher moments indicate an improved reward / risk profile. The skewness is still quite positive while the detrended kurtosis is much closer to a normal Gaussian value.
Bitcoin volatility has fallen considerably
With time, as expected with a power law, Bitcoin’s trend annual return and volatility have fallen substantially. The expected annual return is given by the expression (1 + 1/T)k -1, where T is the age of Bitcoin in years and k = 5.87 is the power law index. Given the current age of Bitcoin, 16.19 years, the expected return is now 42% for the next year

The volatility over the whole history has dropped from over 0.075 per day as shown in Figure 2, to less than 0.05, implying a current daily volatility of less than 0.04. It’s been cut in half during the past 12 years.
Portfolio optimization with two assets: S&P 500 and Bitcoin
To determine optimal allocations in a two asset portfolio of Bitcoin and the S&P 500, including skew and kurtosis one wants to have allocations that minimize:
Return - (portfolio_return / portfolio_standarddeviation) - λ * portfolio_skew + β * portolio_kurtosis
In the MVSK (mean-variance-skew-kurtosis) extension of the Markowitz model, the optimization function is searched for a minimal value. The model favors a higher ratio of return to standard deviation and also favors positive skew (that is desirable), while penalizing positive kurtosis (that is undesirable).
The optimizer solves using nonlinear programming to determine the relative weights for Bitcoin and the S&P index. The optimizer is long only and with maximum asset weight of 100%. I ran the optimizer with modest weights of 0.2 and 0.1 for the λ and β skew and kurtosis terms, however a number of other weight choices led to the same general outcome.
For the S&P, I used the 20-year period skew and kurtosis from Kim and White (2003), the paper linked above that found a skew of -2.39, and I ran the optimization both for the high value of kurtosis and for the much lower value excluding the 1987 crash. The chart below is based on that lower value.

For Bitcoin, since the volatility has dropped so much with time, as has the return to a lesser degree, as consistent with its power law behavior, I used a 4.5 year data period from August 2020 through the end of February 2025 for the analysis. The skew for that period dropped to 1.15 and the kurtosis decreased to 2.91, close to Gaussian. The current expected return is 42.2% in accordance with the power law, and a standard deviation of 0.237 in log10 terms appropriate to the 4.5 year history was used. I used 10% for the S&P typical return and 0.071 in log10 terms (17%) for its standard deviation.
The result was a 100% Bitcoin allocation and the efficient frontier is shown in Figure 3. The lower left is an all S&P portfolio and the upper right an all Bitcoin portfolio. The return rises by nearly a factor of 4 while the standard deviation increases by just over 3 x. The skew is color-coded on the efficient frontier and flips from under -2 to over +1.
Bitcoin wins out because of its advantage in return / volatility and significantly better skew and kurtosis.
Summary
For daily price series, using the conventional daily log return method, Bitcoin has favorable positive skew of 4 and high kurtosis of 25. The higher moments are very large. This is quite different from stocks, whether the S&P or the QQQs, that have negative skew.
If we recognize the fundamental power law nature of Bitcoin and determine residuals by detrending with the power law, then the skew remains positive but is about 2, and the kurtosis is 5 which is moderately fatter than the Gaussian value of 3.
During the most recent 4.5 year period however, the skew is just over 1, and the kurtosis close to 3, near Gaussian.
If we compare to the S&P 500, Bitcoin has an expected return based on the power law of nearly a factor of 4 higher, with a volatility about 3 times higher. Given the skew that is over +1, rather than below -2, a two asset portfolio evaluated by an MVSK optimization algorithm has 100% allocated to Bitcoin.


Hi Stephen.
Excellent March Newsletter.
While I'm quite good with maths. I'm unfamiliar with the tools for investment analysis. I would get much more out of your letter if there was a reference or lead I could follow to read up on the background of these tools.
Many thanks,
Stuart