This is not investment advice. Bitcoin is highly volatile. Past performance of back-tested models is no assurance of future performance. Only invest what you can afford to lose. You must decide how much of your investment capital you are willing to risk with Bitcoin. No warranties are expressed or implied.
Don’t confuse buying time with selling time
Everyone long Bitcoin is concerned about the large price drop during this past year. The Block monthly high was $66,000 less than eight block months ago, and Bitcoin has dropped by a factor of over three since then, to the vicinity of $20,000. The macro backdrop with slowing growth, double-barreled tightening from the Fed and other central banks, and fiscal tightening as well, is very difficult for Bitcoin, which is generally acting as a high volatility risk asset.
But don’t confuse buying time with selling time. Buy low, sell high.
How does one know whether the price is low or high? First, zoom out and look at a full four-year Halving cycle or longer. One must have some type of model, but that model can be regression-free, i.e. not assume any particular mathematical functional curve to be fit.
In this article we look at three regression free models: there is no regression to a model fit, the models are just looking at historical returns.
Block years and months
Each block month is 4375 blocks, or 1/12 of the 52,500 blocks in a block year. A block year is one quarter of the four block year interval between halvings. This is the natural rhythm of Bitcoin and a better calendar choice for models. This approach captures both the halvings and the difficulty adjustments that occur each 2016 blocks more naturally.
Currently 14 block years and one block month have elapsed since Bitcoin began 13 calendar years and five months ago. Block years run slightly faster, but during the past two years, only about three days faster per year.
We are just past the midpoint between the prior halving in May 2020 and the next one in early May 2024 (estimated). Block years currently start in the month of May.
Logarithmic Prices
The long-term trend of Bitcoin is so strong, and the volatility is so high, that one is better off using the logs of prices in models and analyses, rather than modeling linearly. It is a much better way to capture and characterize the high volatility.
Model 1: 48 Month Moving Average
The 48 month average has acted very well as a long term support line. It is typically treated as a 200 week month average, and both averages are close to four years. Since block years are now typically around 50 weeks to 51 weeks long, there is a close correspondence between the duration of block and calendar years, but they have different starting points.
For this analysis I use block months, that exactly fit the halving cycle, unlike the 200 calendar week average. I calculate the 48 block month average (one halving cycle) of the log10 of prices for this model.
I also have calculated the Z-score, the number of standard deviations difference between the actual log price and the moving average of the log price. One notices that the actual price only comes close to the moving average line once with this monthly data. With daily data one will see occasional piercing of the line. The average Z-score over the past 4 block years is 1.29, the minimum is 0.28 and the maximum is 2.72. Bitcoin skews to the right tail, it is a convex asset.
Eyeballing the Z-curve and the actual price line suggest the best time to accumulate is when Z is below one and falling. The next best time is when Z is below one and the Z line is rising. Note that the Z-curve appears to lead price somewhat at peaks, so it may have usefulness as a leading indicator around peaks.
The best time to take profits is when Z is well above 2. But note that after Z reached 2 with almost 9 Block years elapsed, the price rose another order of magnitude.

Model 2: Exponential (e-folding) Model
Like the 48 month moving average model, this e-folding model only uses historical prices, with no regression analysis.
Here we use natural logs for simplicity, and in accordance with the model name, but one could use log10 instead and call it a powers of ten model.
We take the difference of the natural log (ln) of the latest month’s price from the natural log of the price 12 months prior. So if the price has gone up by a factor of e =2.71828, that is one e-fold, or a difference of +1 between the latest ln price and the ln price a year prior.

If we refer to the number of e-folds as y, then y < 0 or near zero, represents the best buying zone. And y above 2 represents a reasonable zone to take profits.
Model 3: Kelly capital growth criterion
This model is about sizing your exposure to Bitcoin. Given the high volatility, when evaluating Bitcoin against cash in a two asset portfolio, one should have more cash than Bitcoin. This is despite the fact that cash has little or no return. Cash is a buffer or hedge against Bitcoin’s high volatility.
This may upset some Bitcoin maximalists, but the recent drop in price by over a factor of three from the prior peak vindicates preserving cash in order to be able to buy when lower prices present themselves.
If you go all in at a relative high point you cannot take advantage of lower prices that become available. And being all in increases the risk of ruin as well as panicking near a bottom. Dollar cost averaging into a core buy and hold position and then adjusting to the Kelly growth criterion should beat other systems most of the time. See
.
It has been well established that the Kelly growth criterion and methodology maximizes growth in portfolio wealth. One sizes the exposure based on historical outcomes and adjusts regularly to keep the exposure near the optimal level. See
.
What one does is look at the historical win rate over a series of ‘bets’. Here I look at each ‘bet’ lasting one block month, i.e. a series of monthly returns. You then look at the fraction of wins p, fraction of losses q, and you calculate the average win size relative to the average loss size, that is called b. So if the average win size is double the average loss, then b = 2.
Table 1. This table shows the optimal portfolio fraction, in retrospect, for each block year of 52,500 blocks in duration. The third block year started right when two block years had elapsed. Currently just over 14 block years have completed. The cyan colored years are the block years prior to a halving, and the green colored are the years following the halving. In each case one of those is the best year in the four-year period centered around the halving. For each block year we show the yearly return, the number of winning and losing months and the average win size for a month and average loss size. The parameter p is the percentage of winning months during the year, q = 1-p is the losing month fraction. And b is the ratio of average win size to the magnitude of the average loss size. The optimal fraction is given by (b*p-q)/b = p - q/b.
The Kelly growth criterion says the optimal Bitcoin fraction of a two asset, cash and Bitcoin, portfolio is determined by win fraction p, loss fraction q = 1-p, and b, the ratio by which wins outperform losses. The volatility is implicitly reflected in the values of p and b. Large b, and p well removed from 1/2 are related to higher volatility.
“The optimal fraction of such a portfolio toward the risky asset is f = (b*p - q)/b, where p is the expected win percentage, q the loss percentage, and b is the ratio of average win size to average loss size. For the trivial case of equal wins and losses b = 1, the optimal fraction is just p - q, so if your expected win percentage were 60% you would allocate 20% of your portfolio” (from my Substack article linked above)
If we just look year by year in Table 1 the optimal fraction bounces around a lot, reflecting the four-year seasonality and volatility of Bitcoin. The optimal fraction ranges from negative in two years to over 3/4. Bitcoin is volatile, so one needs to take a longer term view.
Thus in Table 2 we look at 4, 5, and 10 year averages, to get a better handle on the long term optimal asset fraction, averaging the results shown in Table 1. Over a ten-year period (120 Block monthly ‘bets’), the optimal average fraction is 0.39 or 39% of the portfolio. If we use the prior four years, it is a lower amount, 30% of the portfolio. One might choose 30% as a reasonable maximum, considering that Bitcoin’s price appreciation has been relatively less during the second half of the prior 10-year period. One should continually update this calculation as well as your allocation so that it remains near the desired percentage.
Table 2. Here we summarize the most recent 4, 5, and 10 year averages based on Table 1. Over the past 10 years the optimal fraction of Bitcoin according to the Kelly capital growth criterion has been 39%, as seen in the penultimate column. For the last 4 years, it has been 30% for a full Kelly allocation. The final column gives the expectation for monthly returns. You are unlikely to achieve this, it requires constant rebalancing to the optimal percentage, think of it as an upper limit. No trading fees, slippage, or taxes are considered.
This is the maximum to allocate, and has the best expectation for future growth. A fraction higher than this will not grow your wealth as quickly as the optimal fraction, and your probability of very large losses will increase. If you want to be more conservative you can choose 1/2 or 2/3 of that fraction, say a “half Kelly” or “two-thirds Kelly”.
The methodology here is that you are continually rebalancing to keep your portfolio fraction near the optimal. Thus if Bitcoin’s price drops 10% in a given month and your portfolio fraction drops from 30% to 27%, say, you would buy additional Bitcoin in the following month. You would keep building your position in order to reach the optimal fraction, or 1/2 or 2/3 of the optimal full Kelly if you want to be more conservative. While a full Kelly maximizes expected wealth, it is also subject to significant variability and drawdowns.
Remember, one should regularly update the allocation to keep it near the target fraction of the portfolio.
If Bitcoin’s price goes up significantly, say 20% in one month, and your portfolio allocation exceeds the full Kelly fraction, you would trim your position back to the optimal level. Let’s say you were at 30%. The price increase has taken you up to 36%. You could sell 1/6 of your position and then be back at 30%. Thus the method has you taking some profits when prices are relatively high, and also has you increasing your total wealth. You also retain most of your stack for further long term gains.
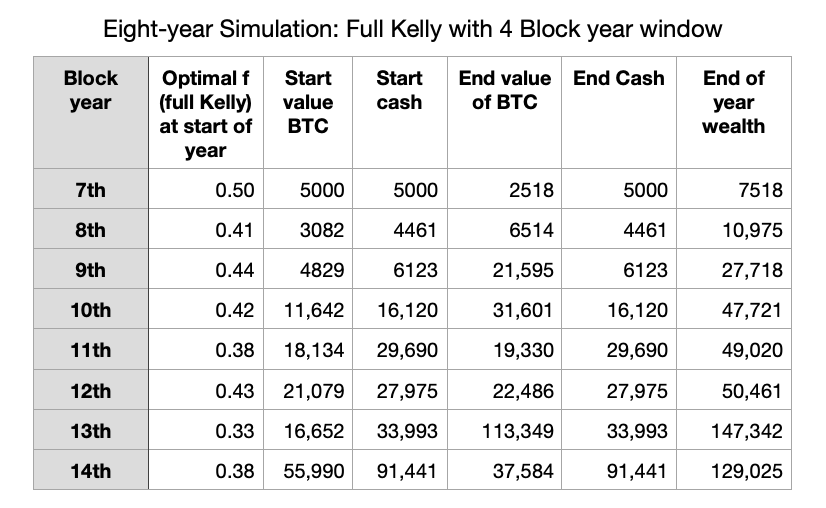
Table 3. Eight year simulation of full Kelly allocation based on prior four years of performance. Adjustment happens yearly. The optimal f is based on the prior four-year average p, q, and b. The starting portfolio is $10,00 and coincidentally is 1/2 of each asset.
Table 3 shows a simulation assuming a starting portfolio of $10,000. The optimal f is based on the average for the prior four years, and for our 7th block year, the first year of the simulation is 0.50. Thus our initial position is half Bitcoin, half cash. That year is a losing year, and it ends with Bitcoin down by nearly 50%, and our wealth drops to $7518. But we prevented a drop all the way down to $5037 if we had allocated 100% to Bitcoin.
At the end of the eight year period we have had two losing years, the first and the last, but each year we are adjusting our Bitcoin fraction f to the prior four years’ performance, our window is one halving cycle. The end result is we increase our capital by almost 13 times to $129,025 for a compound annual growth rate of 38%. If you adjusted monthly or quarterly, you would usually do even better.
While in this particular case a buy and hold at the beginning of the period would outperform, Bitcoin had an extremely good run over that interval, and that may not repeat. The Kelly capital growth model claims to do better in the long run, it keeps adjusting based on historical performance statistics, and you can certainly sleep better at night. Bitcoin’s 24 x 7 “the market is open” reality is both an advantage and a possible cause of insomnia.
Present Situation
Don’t confuse buying time with selling time: buy low, sell high. Bitcoin’s price has dropped precipitously during 2022, down from almost $40,000 at the beginning of this latest block year that started only in early May. It is now $20,745 as I write this.
Table 4 summarizes what these three regression-free models are telling us. Remember, they are not emotional or human, you are. For these models, it’s just math, like Bitcoin’s Nakamoto consensus algorithm with its regular difficulty adjustments and halvings. And these models have a dozen years of price history as input, whereas humans tend to overweight recent events and history. We have to live in the present, but we should not be overwhelmed by it.
The macro backdrop will likely be difficult during the rest of this year and into 2023, so patient accumulation of Bitcoin is warranted.
Table 4. All three of these models suggest accumulation at these low prices, allowing for dollar cost averaging while conditions are favorable. The support line on the 48-month average has rarely been touched, and we are well below the average Z-score. The exponential or e-fold model has a negative score which is in the favorable zone for buys. The last row summarizes a Kelly capital growth analysis, using the last four years of data suggests a full Kelly allocation would be 30% of one’s portfolio (if two assets, cash and Bitcoin) and it would be 15% for a half Kelly allocation.
You can’t manage prices, but you can look at the math, and you can manage your emotions.
References
The Kelly Capital Growth and Investment Criterion, L.C. MacLean, E.O. Thorp, and W.T. Ziemba, editors. 2010, World Scientific Publishing (Chapters 3, 6, 7 by J.R. Kelly, E.O. Thorp, E.O. Thorp).
Understanding the Kelly Growth Investment Strategy, W.T. Ziemba 2016, https://www.caia.org/sites/default/files/AIAR_Q3_2016_05_KellyCapital.pdf