Bitcoin's Power Laws

Fourth Halving Update

This article and the research described within is not, and must not be considered as, financial, investment, or legal advice.

Introduction

The analyses presented here were completed right after the Fourth Halving on April 20, 2024 (UTC). All of the regressions presented have been made in the Block calendar system, that has Block years of 52,500 blocks on Bitcoin’s timechain. Recently block years are very close to Gregorian calendar years in length, but offset, since the recent Halving was in April 2024 after 16 block years had elapsed, but the Bitcoin timechain began in January 2009. The value of using this system is that it aligns more closely with the four year halving cycle behavior that has been observed to date as well as the all-important Difficulty adjustments that maintain the integrity of the timechain and the globally distributed nature of Bitcoin.

Using the block calendar smooths out the difficulty variation since block times vary, often shortening below 10 minutes, but also lengthening on occasion, sometimes to even greater than one hour between blocks. The difficulty adjustment happens in clockwork fashion on block boundaries separated by 2016 blocks. The difficulty algorithm was specifically designed by Satoshi Nakamoto to keep block times close to the nominal 10 minute block time. And it defines difficulty to be linearly proportional to the average hash rate deployed over the prior 2016 block interval. It was motivated by Moore’s Law, knowing that otherwise block times would become very much shorter and the network would lose its ability to remain decentralized across the planet.

Power Laws, not Exponentials

Most financial and economic analysis is done assuming exponential growth using growth rates, inflation rates, discount rates etc.; it is the same thing as compound annual growth at a particular rate (CAGR). For example, over long periods of time the M2 money supply in the United States doubles each decade, corresponding to 7% annual growth on average. If we evaluate 1.07^10 (raise 1.07 to the 10th power), which is a decade of 7% growth, we get a factor of 1.97, basically a double. If the CAGR is in single digits it can be sustained for a long time, but for double digit rates it becomes unstable quickly (think double digit inflation in supermarket prices). Fiat currency lives in an exponential reality.

Power laws and exponentials are quite different things, mathematically. If you try to fit over a shorter time domain perhaps either will appear to work, but the long term behavior is very different.

An exponential relationship has the form: c · exp (t/τ), where τ is the characteristic timescale for exponential growth and c is just a constant multiplier also needed to fit the data of interest. On a log-linear chart (log for the y-axis) this is a straight line. It is very clear from visual inspection of a long-term Bitcoin log-linear price chart, that it is not a straight line, the underlying trend gradually curves downward.

A power law equation is of the form: c · t^k, where there is no characteristic time scale; it is a scaling law characterized entirely by the power law index k and the overall normalization or level, c. There is no exponential growth, and it appears as a straight line only on a log-log chart (both axes display log values). When one plots Bitcoin on such a log-log chart, the essential power law nature jumps out at you. (See Figures 3 and 4 below).

Both exponentials and power laws are two parameter models but their behavior is very different; power laws are more stable in the long term. Nature employs power laws in gravity, electromagnetism, and the nuclear forces (it also has exponential decay with the weak nuclear force, that is the very essence of instability in the natural world).

Many people have heard of the stock-to-flow (S2F) model, which in fact is an exponential masquerading as a power law. The S2F value is equal to 1.0 divided by the inflation rate of the new coinage supply. This model gathered quite a following despite the fact that it must break since it raises S2F, already essentially an exponential stair-step function, to the power of 3. As originally formulated by PlanB it modeled the Bitcoin price as $ 0.4 · (S2F)^3. Now at each halving, looking forward one block year, starting at the first halving and continuing on to the fourth halving, the S2F value was 8, 24, 56, and is now 120; it is converging on a factor of 2 increase each cycle, and that means a factor of 8 jump in price for the S2F model at each halving.

That factor of 8 each four years corresponds to 68% compounded annual growth ad infinitum, which is clearly unsustainable. The model is now broken at the fourth halving, if not before, since it evaluates to $691,200 and that is over 10 times the current price, or well over three standard deviations from the trend of the well-performing and more statistically robust power law model.

The physicist @Giovann35084111 (Giovanni Santostasi, ”PlanG”) was the first to introduce power law modeling for Bitcoin a decade ago. PlanG has developed a full theory around Bitcoin adoption (addresses holding Bitcoin are the measure here) and hashrate of mining as the principal intrinsic drivers, and those quantities display power law behaviors of their own.

I independently started using power law modeling for Bitcoin in 2019 without being aware of PlanG’s earlier work. I have found that the best models to work with are power law and S-curve models, using the Weibull cumulative distribution function for the latter, and they are equally statistically robust. In the early years of a Weibull S-curve it reduces precisely to a power law in any case.

There is little need for the additional complexity (one more parameter) of the S-curve models unless the power law would start to break down. Its clear persistence over the last 15 years for an increase of 7 (8) orders of magnitude in price (market capitalization) suggests excellent longevity and a path to a very high market cap into the many trillions of dollars in the years ahead. S-curves might come into play when approaching $100 trillion market cap, or roughly 10% of all global wealth today.

Regressions show Power Law behavior

All of the regressions reported here are of the form P = c · B^k (the kth power of B) , or equivalently, log P = log c + k log B, where P is some dependent variable (e.g. price P) and B is the independent variable (e.g. block years elapsed, a time variable.) With this form k is the power law index, it measures the steepness of the power law, and c is a scaling constant or equivalently log c is the intercept. If the relation is a power law then log P is linear in log B and when plotted on a log-log chart the best fit regression appears as a straight line of slope k. We use log base 10 throughout and regressions were performed with the StatPlus package.

Table 1. Log-log regressions of price and market cap against age of Bitcoin in Block years, for the entire data set from age 1 year to 16 years and also for the interval from 4 years (first halving) to 16 block years (fourth halving),

The results of several of the regressions, using data on half-year intervals, are summarized in Table 1. We did a sensitivity analysis by using only yearly data and the results were similar.

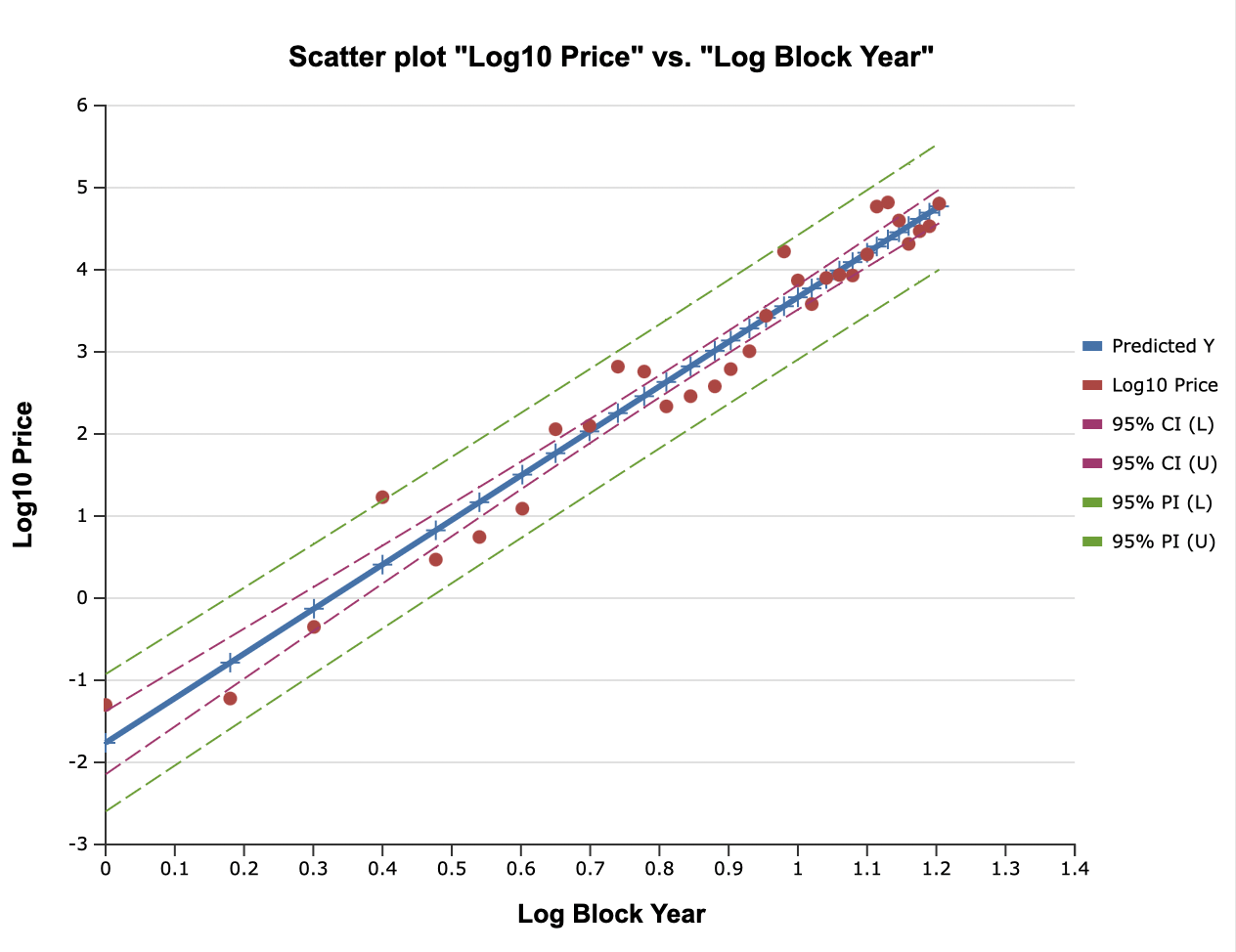
Figure 1. Log-log graph of Bitcoin Price vs. Block Years, with power law index of 5.43 for the power law relationship. The 95% (two standard deviation) range is shown with green dashed lines. Note that values below the trend are typically within one standard deviation (at most halfway to the green dashed line below), whereas positive excursions extend to two standard deviations (fully upward to the green dashed line above).

For the full data sets, we find a power law index k of 5.43 for the price relationship and 6.44 for the market cap. In the early years the coin supply was growing quite rapidly, with inflation above 4% until the second halving, so we expect a higher value for market cap. But they should converge over time. So we also ran regressions starting from year 4 and above. For those the price index was slightly higher at 5.51 and the market cap index was much closer to the price index, at 5.96.

The R-squared values of correlation are quite good in all cases, as are the F-test values. And the errors on the power law indices are only at the few percent level.

I also ran regressions on the address count over time, using addresses holding over one BTC. We chose this level because of the wide variation in balances in addresses and because 93% of all Bitcoin is contained in addresses of 1 BTC or larger. Here we found a power law behavior as well, with index 1.35 and a very high R-squared value and F-test result. The same was true for the difficulty parameter, and it has a very steep 11.36 power law index, with an error of only 2% in the index value. This reflects the much faster than Moore’s law progress that has been seen in mining rig performance as well as the rapidly growing count of now several million machines dedicated to the Bitcoin minting business.

Bitcoin actually is built on a foundation of power laws, that includes both Metcalfe’s Law for network growth and Moore’s Law, but with a difficulty control mechanism added in order to avoid excessively short block times as a result of technology growth. It also has a control mechanism that dampens exponential bubbles. PlanG has identified this as selling by long-term HODLers at favorable prices around peaks, that tend to occur at around two standard deviations in the right tail of the price distribution (Z around +2).

Figure 2. Log-log graph of Market Cap vs. Block Years, with power law index of 6.44 for the power law relationship. The 95% (two standard deviation) range is shown with green dashed lines.

Figures 1 and 2 show the excellent fits in the form of log-log charts for price and market cap. Both exhibit straight line behavior on such graphs, as expected for power law relationships. The green dashed lines are the two standard deviation contours, and one can note that the price is positively skewed; it tends to not drop much below minus one standard deviation and never reach the lower green dashed line, but often rises to plus two standard deviations, to meet the upper dashed line.

Summary

In summary we have very strong power law trends in difficulty and address growth as well as in the price and market cap for Bitcoin. These all have R-squared values of 0.96 or better (or better than 0.90 with the restricted data set from age four years). Market cap grows at around the 6th power of block time and price grows as the 5.5 power approximately. The error in the index for each of market cap and price is just 0.21, only 3 or 4 percent (or 6% with the restricted data set).

The regression of addresses, measuring adoption, and difficulty (or hash rate) are extremely strong statistically with R-squared values of 0.98.

On balance the trends for both price and market cap are very strong, and firmly based on and confirmed by underlying power laws for both difficulty and addresses. Thus it is quite reasonable to expect the power law behavior to persist through the fifth halving in 2028 and sixth halving due in 2032. While it is possible that the power law may become less steep at some point, signaling a transition to an S-curve as I have modeled elsewhere (using the Weibull function) I don’t expect that to happen until after the next halving at earliest, and perhaps not until Bitcoin reaches a market cap in the vicinity of $100 trillion or more.

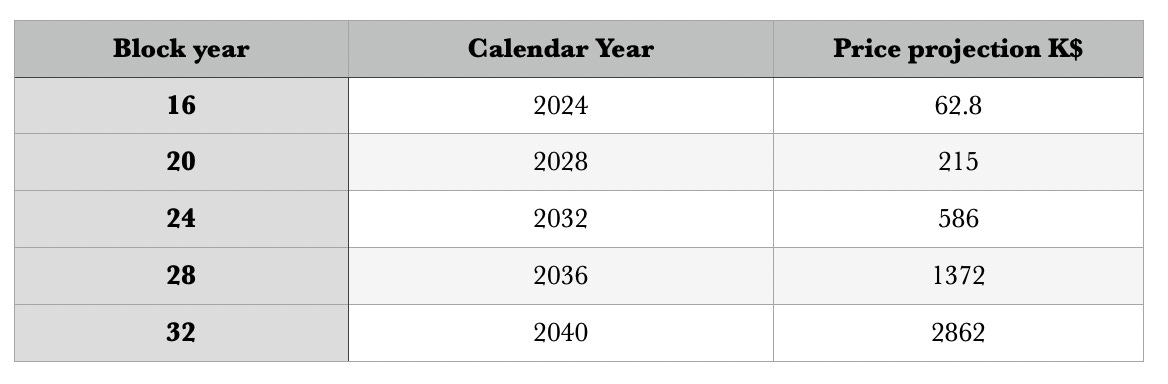
In Table 2, I show the price projection of the power law trend for fair value, assuming a power law index of 5.51. One could reach the $1 million price point in just over 10 years, and sooner with a one or two standard deviation upward excursion. The single standard deviation is 0.32 in the log10 or higher, which is a multiplicative factor of 2.09.

Table 2. Price projection of fair value based on power law of index 5.51 and regression from 4 to 16 block years. The $1 million price point in this model is about 10 to 11 years from now. One could guesstimate future inflation at about 7% in the USD M2 money supply, which is the historical compound annual growth rate. That would mean $2.86 million in 2040 could be worth about $1 million in current dollars. With the same estimate the $586K in 2032 would be worth about $341K in today’s dollars.