This article and the research described within is not, and must not be considered as, financial, investment, or legal advice.
Monthly return has fallen a factor of four
It is objectively the case that both the rate of return on Bitcoin, and its volatility, decrease with time. It is manifestly the case when examining the price history and without the need to apply any particular model for price behavior.
To construct the table below, we have looked at the series of block monthly returns since Bitcoin was one block year of age. Each block month is an equal twelfth of a block year of 52,500 blocks, and there are four block years per epoch. As of the fourth Halving of the Bitcoin block subsidy on April 20, 2024 (April 19th in the Americas), there have been four completed epochs of 210,000 blocks.
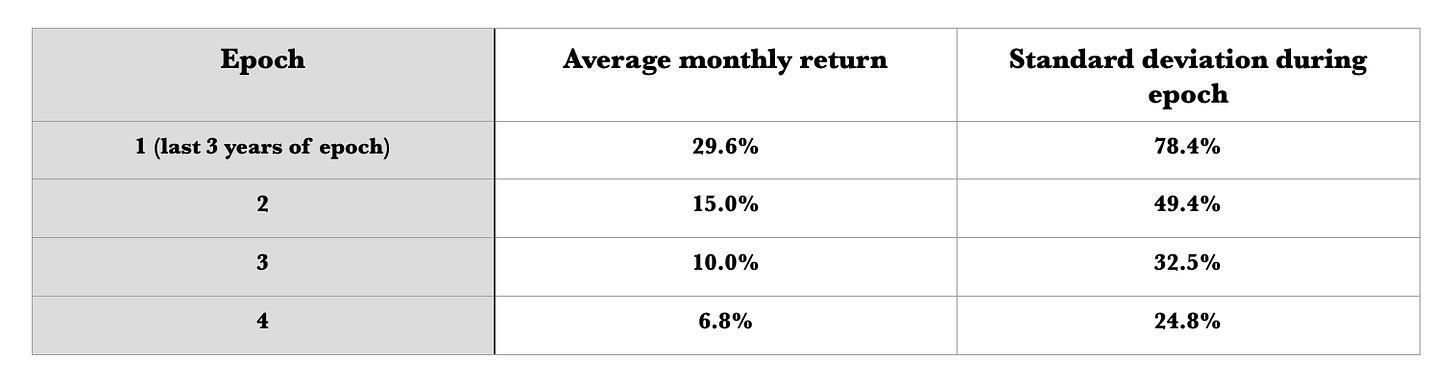
Table 1. Bitcoin average monthly return and volatility (standard deviation of monthly returns) by epoch.
Figure 1. Bitcoin average monthly return (orange line) and volatility (blue line).
The figure makes it clear. The average monthly return fell in half from Epoch 1 to Epoch 2, by 1/3 from the second to the third, and by another 1/3 as we reached Epoch 4. Epoch 4 was just completed two weeks ago. So from Epoch 1 to Epoch 4, the average return fell by about 3/4.
The volatility has also decreased substantially with each epoch, falling over 1/3 from the first to the second and about 1/3 from the second to the third. For the just completed epoch, it fell by 1/4. Volatility has dropped by more than a factor of 3.
And yet Bitcoin’s volatility remains three times or more the average monthly return. This is why it is so difficult to trade and it is better approached as a long-term asset holding, not only not a trading vehicle, but not an ‘investment’, rather as long-term savings held over a full epoch or longer.
Power Law agrees
In table 2 I repeat the observations in table 1 but also add columns for a straight power law calculation of projected performance as well as for a power law projection plus diffusion, which also accounts for positive skew of returns (fat right tail). And I add a fifth row for the estimated return for this current Epoch 5. Let’s explain.
Table 2. Bitcoin average monthly return from the power law projection (next to last column) and incorporating a correction for positive skew that increases the return (final column).
Since with the power law model, price ~ B^k, where B is block years elapsed since Bitcoin began, and k is the power law index of best fit to the data, one can project the expected percentage of fair value price increase during the following year.
One can immediately see that as B grows larger for a fixed k, the 1/B term decreases and the expected return gradually drops.
I calculate the expected monthly return by taking the 12th root of 1 plus the annual return as a fraction, then subtracting 1 and converting to percent. We see the monthly numbers calculated from the model for each epoch in the fourth column. They exhibit the right trend but are consistently too low by approximately a factor of two for Epochs 2, 3, and 4.
There is a reason for the average monthly returns being higher than the power law projection, and that is the bubbles, the very positive excursions, that have caused the price to run up by factor of several at various times. And in addition, the long term drops in Bitcoin are capped. It can go up by substantially more than 100% but it can never fall more than 100% (despite Peter Zeihan’s prediction of a negative price). And in fact maximal drops are around 67%.
Figure 2. Q-Q plot of residuals of monthly Bitcoin returns relative to the best fit power law. The residuals are quite positively skewed with a sharp cutoff for the left tail in the area of -0.4 to -0.5 for the log10 value. The right tail has no such cutoff and extends beyond the maximum expected value.
The residuals are quite skewed, normality is rejected by the Shapiro-Wilk test to a chance of one in a hundred thousand. There is a sharp cutoff on the left tail at around -0.4 to -0.5 in the log10 or a factor of 2.5 to 3 down from the trend; in other words a maximal drop of -60% to -67% or so. The positive right tail is favored with upside as high as log10 of 0.6 to above 0.8, corresponding to multiplicative factors of 4 to 7 (positive excursions of 300% to 600%). This positive skew in residuals adds to the upward bias of prices.
“If a return distribution shows a positive skew, investors can expect recurrent small losses and [a] few large returns from investment. Conversely, a negatively skewed distribution implies many small wins and a few large losses on the investment.” - Corporate Finance Institute
And this, in two sentences, is why it is better to be a long term investor in Bitcoin. You have to stick around for the big wins and for the power law to overcome the high volatility.
Incorporating skew means we have something like a convection - diffusion process in nature, with a bulk velocity plus a net diffusive velocity (since positive skew) that tends to move in the same direction as the bulk flow. As a quick and dirty method we note that that there are 8 data points out of 169 (4.7% of them) that exceed two standard deviations in the right tail (the few large returns). There are no such data points exceeding two standard deviations in the left tail.
The gross return rate R in this simple model is thus a function of the expected power law return r, plus a diffusion coefficient that we take to be f = 0.047 and that is multiplied by the square of the standard deviation ( σ ). It’s a square root of the sum of the squares with a small diffusion coefficient that reflects the amount of positive skew.
This power law with diffusion estimator, whose results are in the last column of Table 2, generates values similar to the observed values, but underestimates those to some degree. What is going on is that the bubbles push the price level upward and when they burst, price falls back below trend but not as much and a new price floor is established going forward. While this admittedly crude model slightly undershoots the observations, the basic idea appears sound that the positive skew adds several percent per month to the actual total return.
In any case, the main point is that with the power law of time behavior of Bitcoin, the return does drop monotonically and appreciably from one Epoch to the next. And the second key point is that the expected return is still so high that we should have excellent long-term returns for decades to come.
Figure 3. Log10-log10 graph of Bitcoin price vs. age of timechain in block years and the best fit power law regression line. The green dashed lines are the two standard deviation contours. Note that eight of the data points exceed two standard deviations on the positive side, but the downside two standard deviation line is never reached. The residuals are significantly skewed to the right (positive) tail.
Projections for Epoch 5
For the present value of B = 16 and k = 5.5, the expected return for the next year is 38.7%. That is a monthly return of 2.77%. The projected annual returns for the second through fourth years of the Epoch are 36.2%, 33.9%, and 31.9%. The respective monthly compounded returns for each of those years are 2.61%, 2.46%, and 2.33%.
Thus the expected average monthly return over the epoch 5 would be 2.54% plus the effects of skew. And the projected total four year return for our new Epoch 5 is computed directly as
= 234%. That is a compound annual rate of 35.1% and a monthly compounded rate of 2.54%, note the agreement with the other calculation for the average. One might expect volatility would drop by 1/4 or more, which could place it around 19%.
So in the table above, in the last row for Epoch 5 I estimate the total average monthly return, including the effect of positive skew, to be near 4.8%.
Yes the returns are slowing, but as monthly returns, these are extremely attractive. The positive skew means HODLers do better than traders, one expects a few very high return months that are outnumbered by a large number of down months or months with less than average performance.
When does Bitcoin asymptote?
It is interesting to consider when Bitcoin’s expected return will drop to 10% which is the long term rate of return on the S&P 500. We’ll see that we have a lot of outperformance ahead of us.
Ignoring the skew effects, which should continue to decrease, this is simply solving:
Equivalently, for k = 5.5,
Or B = 57, which is 41 block years from now.
There are still 10 more halving epochs of superior performance ahead if the power law holds with around the same index as today or better. Unless the S&P 500 companies adopt Bitcoin into their treasuries in a substantial way as Michael Saylor advocates.
And what would Bitcoin’s market cap be by then? The price would be about today’s price of $64K times (56/16)^5.4 or 867 times higher, some $55 million and the coin supply would be very close to 21 million by then. It works out to $1.2 quadrillion which is more than global wealth today. However this does not correct for inflation in the money supply that runs about 7% for the US dollar.
The dollar’s buying power typically gets cut in half once each decade. After four decades that is a factor of 16! If we take 55 million x 21 million and divide by 16 one has $73 trillion in 2024 dollars and that is 3/4 of the present global M2 money supply.
Currently that world money supply of $100 trillion (in various currencies include USD, Euro, Yen, Yuan, Pounds, etc.) is sufficient to support a global GDP of about $110 trillion and to denominate global wealth of $900 trillion.
Over several decades Bitcoin’s value could grow to become the dominant monetary unit of account, a monetary standard. At that time its network value would exceed $1 quadrillion in a world of perhaps as much as $10 quadrillion of global wealth.
Bitcoin could put the global economy on a surer footing; today it is all built on a fiat monetary system of only debt, but Bitcoin is better: a true asset, absolutely finite, secured by substantial energy and strong cryptography to the tune of over 600 decentralized Exahashes/second.







I'm pretty surprised your work hasn't received more attention. It definitely should. Came here from one of your recent tweets, so thanks.
Thank you for your thoughtful analysis of the Power Law and its effects on inflated dollars, and also such a long term perspective — most analysis stops around twenty years out.