Bitcoin is the Best Asset Class

Kelly Criterion suggests a 75% portfolio allocation

Kelly criterion

The Kelly criterion was developed by John Kelly of Bell Labs in the 1950s. He was an associate of Claude Shannon, who determined the entropy of information and made major advances in signal theory at Bell Labs in the prior decade. The Kelly criterion is a consequence of Shannon’s information theory when applied to games of chance or investments.

Figure 1 is the curve of a particular case with a probability of p = 0.6 and with an even ratio b = 1 for win and loss payoffs, q = 1- p is the fractional percentage of loss events. In line with the Kelly formula f = p - q/b = 0.6 - 0.4/1.0 = 0.2 the curve of growth rate says the the optimal bet size is 20% of the portfolio. Betting over 20% is suboptimal and if one bets over 38% you lose money on average. This is because of the asymmetric nature of win and loss percentages.

Figure 1. Curve of growth rate of a portfolio as a function of wagered fraction or portfolio allocation, for the case p = 0.6 and b =1. The optimal bet is just 20% of your portfolio, betting more is sub-optimal.

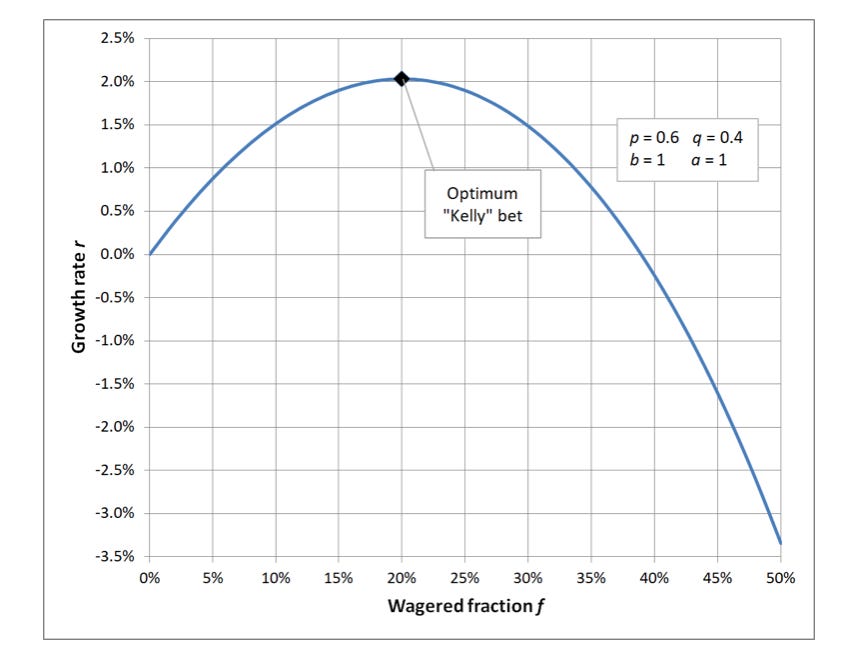
If you ignore the guidance and allocate 33.3% on the first bet then you have to win 50% to get even. Bet 40% and lose twice in a row? You are down to 36% of your initial stake and would have to gain 178% to get back to even. With repeated bets you keep adjusting the bet size in absolute terms to the optimal percentage (which can also change as you gather more data).

This URL https://theory.stanford.edu/~blynn/pr/kelly.html provides an overview of the Kelly criterion and even has a game online that you can play to convince yourself. A group of five dozen investment professionals on the whole failed the optimal Kelly test, even though they were provided with a p = 0.6, b =1 edge and told the odds. In an experiment conduced with finance professionals and quants, 1/3 of them went bust.

The Kelly wealth optimization criterion deals with the asymmetry problem by optimizing the growth of log wealth in the long term. This leads to the derivation of optimal f, which says if you bet a fraction f and win you gain f * b and your new portfolio has increased by the factor 1 + f * b. If you lose, your portfolio shrinks by the ratio 1 - f.

So deriving the optimal Kelly f is a matter of finding the maximum of the expected growth rate of wealth as a function of f, the fraction of the portfolio that is bet.

E <Log W> = p* log (W₀ * (1 + b*f)) + q * log (W₀* (1-f))

Here W is the wealth after some statistically sufficient number of trials and W₀ is the initial wealth. E <Log W> is the expectation value for log W. Its maximum is found by taking the derivative of the right hand side with respect to f.

Figure 2. Outline of the derivation of optimal Kelly f. W0 is starting wealth, p is the win percentage and b is the payoff advantage of wins relative to losses. There is an assumption that p and b have stable average values over many bets.

The result is that the optimal bet size is f = p - q/b. The assumption is that p and b are stable over long periods of time. The best opportunities have two edges, p > 0.5 and b > 1, and the more so the better.

For a portfolio with only cash and a risk asset, f is the optimal portfolio allocation and may depend on the time interval chosen (ahead of time) for decisions. One recomputes the optimal f as new information comes in, in order to adapt to current values for average win probability p and payoff ratio b.

For investments, do you look at weekly, monthly, quarterly, or yearly intervals, for example. In the case of Bitcoin, longer holding periods indicate much higher allocations, as the signal wins out over the noise, despite its substantial volatility.

The Kelly principles are avoiding run, and balancing the utility of wins vs. losses, and result in long term growth of log wealth.

A decade of major asset classes

Table 1. This shows the annual returns for 16 asset classes over the past decade. Bitcoin was in the #1 position for 8 out of 10 years, which is unheard of. It also was in last place in two of the years.

Table 1 shows ten years of annual returns for major asset classes. Eight of these are bonds, most of the rest are equities, and gold and commodities are included as well. One of the equity classes is REITs. There is nothing to compare to Bitcoin as an asset class, it had far and away the highest return and won first place in eight out of 10 years.

Optimal f for the 8 non-bond asset classes

Table 2 summarizes the Kelly optimal fraction f calculations for all of the 8 asset classes other than bonds, none of which was particularly lucrative. The p and b values are shown in the second and fifth columns.

Bitcoin is the best as shown in the 6th column with a optimal f of 0.75. Broad tech has been second, and large caps third. Commodities were actually negative. Even if you are concerned that Bitcoin cannot repeat the returns of its early years, just the second half of the period, 5 years of data, still has f = 0.71.

One can also correct for the risk-free cash rate, I chose r = 4%. The adjusted b* and f* are shown in the final two columns, Bitcoin remains at f of 0.75 and even limiting to the last 5 years it only decreases slightly, to f = 0.70.

Once you adjust for r, four of the asset classes switch to negative allocation percentages vs. risk-free cash during the past decade. The large cap allocation drops from 0.53 to 0.40. The gold allocation drops from 0.36 to 0.09.

Table 2. For the eight non-bond asset classes and the past decade of annual returns, this table shows the probability p of a win, the average % win size w, the average % loss size l, and the win/loss edge b = -w / l. The optimal fraction f is then simply p - (1-p)/b. The last two columns also include the effects of a risk free rate of return r = 4%.

Kelly strategy takes grit, can reduce to 1/2 Kelly or 2/3

John Kelly was quite the character. Sadly he died young. Read this short bio and you will likely be convinced he would be a Bitcoiner if he were around today. https://home.williampoundstone.net/Kelly.htm

If you are uncomfortable with a full Kelly allocation you might consider a half Kelly. William Poundstone writes:

“By always making the Kelly bet, you increase your bankroll faster than with any system. That's the good news. The bad news is that it's a rough ride. Downward plunges of wealth are frequent and steep… For the lone player betting on a single hand or horse, the Kelly formula demands guts and patience -- hence the controversy. Many have found the "half Kelly" strategy to be a good compromise. You bet half of edge/odds. This achieves ¾ the compound return of Kelly betting with much less volatility.”

For more discussion around fractional Kelly strategies, as a result of uncertainty in the knowledge of p and b, see: https://matthewdowney.github.io/uncertainty-kelly-criterion-optimal-bet-size.html?utm_source=chatgpt.com .

For myself, Bitcoin has had 13 rolling 4-year periods, and every one of those has been a substantial winner. It’s on a power law trajectory, and a very steep one, as has been repeatedly demonstrated by Giovanni Santostasi, myself, and many others, and is headed toward $1 million.